[python_파이썬_공배수 시간복잡도_유클리드호제법]백준_1934번_최소공배수_풀이

공부하는허딩크 : https://www.youtube.com/live/0PBsmU7Tfk4?feature=shared

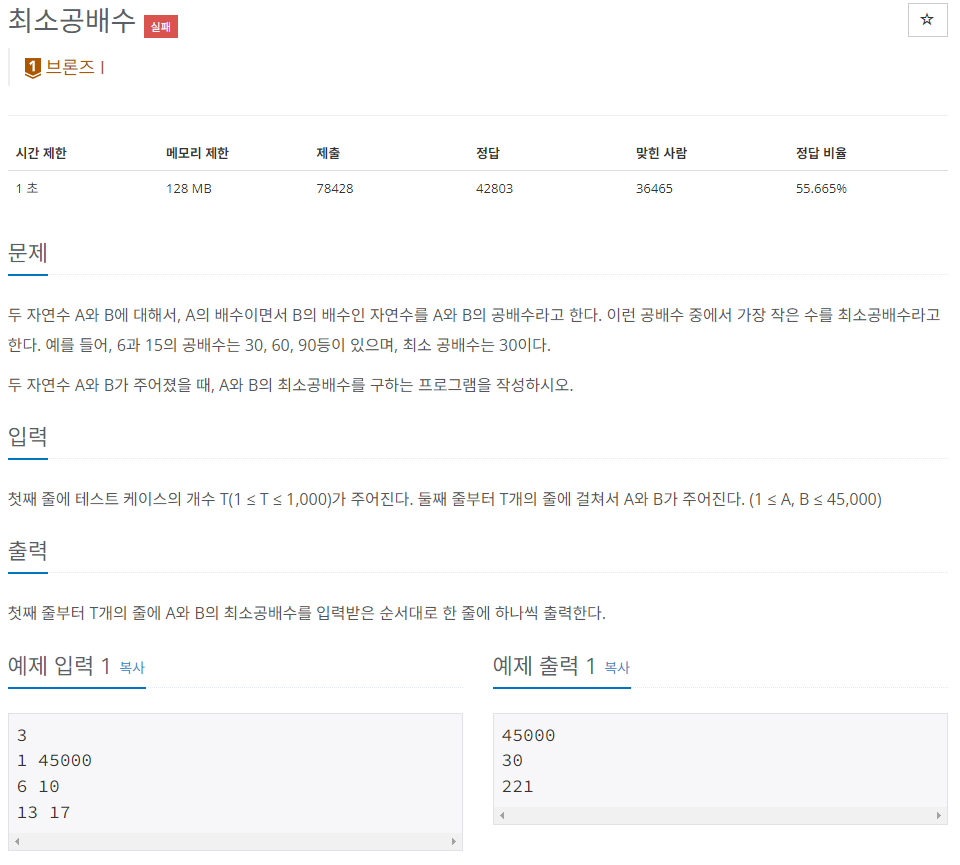
일단 수학적 지식 없이 코드를 작성해보자. 
개인적으로 함수나 알고리즘 없이 생각나는대로 작성하는 것을 선호한다.
 
<첫번째 시도 : 시간초과 : 안될거 생각하고 함_시간복잡도 O(B)>
파이썬 프로그램을 돌려도 한참 뒤에 출력이 된다 => 그래서 코드가 오류인줄 알았음

import sys

input = sys.stdin.readline

#최소공배수: 알고리즘 없이 그냥 생각나는대로....

T = int(input())

for _ in range(T):

    A, B = map(int, input().split())

    A, B = min(A, B), max(A, B)

    B_list = []

    cnt = 1

    while A * cnt not in B_list:

        B_list.append(B * cnt)

        cnt += 1

       

    print(A * cnt)

 
<두번째 시도 : 시간 초과_시간복잡도 O(A+B)>
최소공배수를 구하려면 A * B // 최대공약수를 해주면 된다.
예시에도 나오듯이
1 * 45000 // 1 = 최소공배수 45000, 최대공약수 1
6 * 10 // 2 = 최소공배수 30, 최대공약수 2
13 * 17 // 1 = 최소공배수 221, 최대공약수 1

import sys

input = sys.stdin.readline

#최소공배수는 A * B / 최대공약수

T = int(input())

for _ in range(T):

    A, B = map(int, input().split())

    A_list = []

    B_list = []

    same = []

   

    for i in (A, B):

        for j in range(1, i + 1):

            if i % j == 0 and i == A:

                A_list.append(j)

            elif i % j == 0 and i == B:

                B_list.append(j)

   

    for i in A_list:

        for j in B_list:

            if i == j:

                same.append(i)

    print(A * B // max(same))

 
<세번째 시도 : 시간초과_시간복잡도 O(A + B)>
컴프리헨션과 이중for문 그리고 각각 for문을 한번씩 사용해도 시간복잡도는 동일하다고 한다. (from chat gpt)
set과 intersection으로 교집합을 구한 뒤 최대공약수를 구해서 계산해도 시간초과가 나온다.

import sys

input = sys.stdin.readline

#이중for문 최대한 피하기

T = int(input())

for _ in range(T):

    A, B = map(int, input().split())

    A_list = [i for i in range(1, A + 1) if A % i == 0]

    B_list = [i for i in range(1, B + 1) if B % i == 0]

    same = set(A_list).intersection(set(B_list))

    print(A * B // max(same))

 
<네번째 시도 : 틀렸습니다.>
최대공약수를 찾는 방법을 찾던 중 범위를 제곱은으로 한정하면 시간 복잡도가 감소한다.
단, 최대공약수를 찾지 못하는 수들이 있다. 36과 48의 경우 최대공약수는 12이나 제곱근으로 범위를 구할 경우 6이 나온다. (유클리드호제 알고리즘을 피하기 위해서 이것저것 다 해본다)

import sys

input = sys.stdin.readline

#이중for문 최대한 피하기

T = int(input())

for _ in range(T):

    A, B = map(int, input().split())

    A_list = [i for i in range(1, int(A**0.5) + 1) if A % i == 0]

    B_list = [i for i in range(1, int(B**0.5) + 1) if B % i == 0]

    same = set(A_list).intersection(set(B_list))

    print(A * B // max(same))

 
<다섯번째 시도 : 시간초과 :list를 사용하지 않고 set을 사용했는데 역시나....>

T = int(input())

for _ in range(T):

    A, B = map(int, input().split())

    A_list = set(i for i in range(1, A + 1) if A % i == 0)

    B_list = set(i for i in range(1, B + 1) if B % i == 0)

    same = A_list.intersection(B_list)

    print(A * B // max(same))

 
<여섯번째 시도 : 맞았습니다._시간복잡도 : O(A+B)>
B_list의 약수를 구하지 않고 바로 A_list의 약수들 중에서 큰 것부터 뽑아내면서 B요소와 나누어 약수의 조건을 만족시키면 break를 걸었다.
시간복잡도는 차이가 나지 않아도 break때문에 조기 종료되서 통과가 가능한가?? => 이건 정확히 모르겠네.

import sys

input = sys.stdin.readline

T = int(input())

for _ in range(T):

    A, B = map(int, input().split())

    A_list = [i for i in range(1, A + 1) if A % i == 0]

    A_list.sort(reverse=True)

   

    for i in A_list:

        if B % i == 0:

            answer = i

            break

    print(A * B // answer)

 
<유클리트호제법_Euclidean algorithm>
파이썬의 정수론은 정수에 대한 수학적 속성과 구조를 연구하는 학문이다.
1. 소수론 : 소수의 분포, 소수의 특성, 소수를 이용한 암호화등
2. 합성수 분해 : 주어진 정수를 소수의 곱으로 분해하는 과정 => 암호학에서 중요한 역할
3. 최대공약수와 최소공배수계산
4. 모듈러 연산 : 정수를 어떤 정수로 나눈 나머지
5. 페르마의 소정리와 오일러의 정리등
6. sympy, numpy : 라이브러리
7. 내장함수 : math모듈, 내장연산자(%)
8. math모듈 : math.gcd()가 최대공약수 구할 때 활용 => 유클리드호제법
9. math모듈의 주요 함수 : math.sqrt(x) : x의 제곱근을 반환, math.pow(x, y) : x의 y 제곱을 반환.

1. 수학 함수:
   • math.sqrt(x): 제곱근을 반환합니다.
   • math.pow(x, y): x의 y 제곱을 반환합니다.

<math.gcd활용 : 시간 복잡도 O(T log(max(A, B))) ==> 위에 코드는 O(T max(A, B))>
시간이 너무 차이나는데???

import sys

import math

input = sys.stdin.readline

T = int(input())

for _ in range(T):

    A, B = map(int, input().split())

    answer = math.gcd(A, B)

    print(A * B // answer)

 
<상세 코드 : 코드는 이해하겠는데 원리는 잘 이해가 안되네....>

def gcd(a, b):

    while b != 0:

        a, b = b, a % b

    return a

a = 6, b = 10일 경우, b == 0일때 멈춤 ==> a = 2

a	b	<=	b	a % b
10	6		10	6 % 10 = 6
6	4		6	10 % 6 = 4
4	2		4	6 % 4 = 2
2	0		2	4 % 2 = 0

 <GCD논리 : 결론 최대 공약수 그냥 외우자.>
두 수 A와 B의 최대공약수(GCD)가 B와 나머지 R의 최대공약수와 동일한 이유는 유클리드 알고리즘이 수학적 성질을 이용하기 때문입니다. 이 성질은 다음과 같은 논리에 기초합니다:

기본적인 원리: 공약수의 성질

A와 B의 최대공약수를 구하려면, 두 수 A와 B를 공통으로 나누는 가장 큰 수를 찾아야 합니다.

만약 어떤 수가 A와 B를 동시에 나누는 공약수라면, 그 수는 A를 B로 나눈 나머지 R도 나누어야 합니다. 반대로, R과 B의 공약수 역시 A를 나눌 수 있습니다.


이유를 단계별로 설명:

1. 두 수 A와 B가 있다고 가정해봅시다. 여기서 A > B라고 가정하고, A를 B로 나눈 나머지를 R이라고 하겠습니다.

A = B × q + R  (여기서 q는 몫이고, R은 나머지입니다)



2. A와 B의 최대공약수를 G라고 합시다. 즉, G는 A와 B의 공약수이며, G는 A와 B를 나눌 수 있습니다:

A = G × x (어떤 정수 x)

B = G × y (어떤 정수 y)



3. R은 A에서 B를 나눈 나머지이므로 다음과 같이 나타낼 수 있습니다:

R = A - B × q

R = G × x - G × y × q

R = G × (x - y × q)


즉, R도 G의 배수입니다. 따라서 G는 R도 나눌 수 있습니다.


4. 결론적으로, A와 B의 최대공약수는 B와 R의 최대공약수와 동일합니다. 따라서 A와 B의 최대공약수를 구하는 문제는, 더 작은 두 수인 B와 R의 최대공약수를 구하는 문제로 변환될 수 있습니다.



이 과정을 반복해서 나머지가 0이 될 때까지 진행하면, 결국 최대공약수를 구할 수 있게 됩니다.

예시로 다시 설명:

A = 48, B = 18이라고 가정하면:

48 ÷ 18 = 2 (몫), 나머지 R = 12

48 = 18 × 2 + 12이므로, 48과 18의 최대공약수는 18과 12의 최대공약수와 동일합니다.

다음으로 18 ÷ 12 = 1 (몫), 나머지 R = 6

18 = 12 × 1 + 6이므로, 18과 12의 최대공약수는 12와 6의 최대공약수와 동일합니다.

마지막으로 12 ÷ 6 = 2 (몫), 나머지 R = 0

나머지가 0이므로, 12와 6의 최대공약수는 6입니다.



따라서 48과 18의 최대공약수도 6이 됩니다.

이 성질 때문에 유클리드 알고리즘은 매우 효율적으로 최대공약수를 구할 수 있는 방법이 됩니다.




<다른사람풀이 참고>
1. 거의 유클리드호제법으로 구하는게 대부분이다.
  단, a >= b일때 a, b = b, a로 해서 그 이후로 유클리드 호제법을 사용한다.
2. 나처럼 유클리드 호제법을 사용하지 않는 코드들이 몇개 있는데 참신하네 (시간은 4652ms)

T = int(input())

for i in range(T):

    arr = list(map(int, input().split()));

    arr.sort();

    n = 1;

    for j in range(1, arr[1]+ 2):

        if (arr[0] % j == 0 and arr[1] % j == 0):

            n = j;

    print(arr[0] * arr[1] // n);