[python_파이썬_Fail]백준_1789_수들의 합_투포인터, 그리디 알고리즘_풀이

공부하는허딩크 : https://www.youtube.com/live/dnKTEnrL2OM?feature=shared

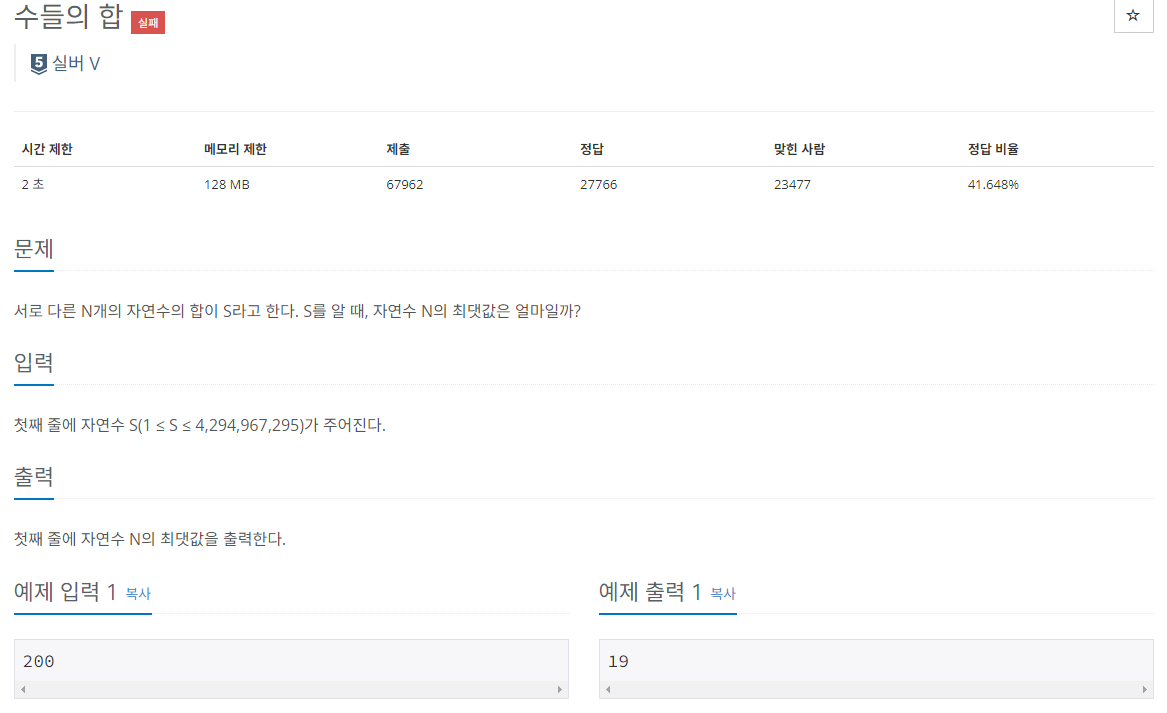
투포인터 알고리즘 쉽게 봤다가 2시간 30분째 해매고 있다.

 

실버5정도 문제인데 답이 안나오네. 문제를 읽고 모든 경우의 수 itertools로 해결하려고 했는데 파이썬에서도 memoryError가 나오네.

 

<첫번째 시도 : 메모리 초과>

고민하면서도 과연 itertools로 부르트포스 알고리즘 처럼 모든 경우의 수를 한번씩 다 확인하는 작업이어서

문제의 범위가 4, 294, 967, 295이므로 안될 걸로 예상했다.

import sys

import itertools

input = sys.stdin.readline

"""N개의 자연수의 합_N의 최댓값"""

S = int(input())

s = list(i for i in range(1, S + 1))

cnt = 1

ans = 0

while cnt <= S:

    nums = list(i for i in itertools.combinations(s, cnt))

    for j in nums:

        if sum(j) == S and len(j) > ans:

            ans = len(j)

    cnt += 1

   

print(ans)

공부를 더 열심히 해야 겠네.

될때 까지 때려 박아야지.

 

<두번째 시도 : 정답이 안나온다.>

어차피 1, 2, 3, 4, ..... 이렇게 자연수들이 있고, 

마지막에 남은 숫자와 위에 자연수들의 개수를 구하면 될 것 같았다.

정답은 21이 나와서 아니다.

import sys

import itertools

input = sys.stdin.readline

"""N개의 자연수의 합_N의 최댓값"""

S = int(input())

answer = 0

start = 1

cnt = 0

while start < S:

    S -= start

    start += 1

    cnt += 1

print(start + 1)

   

 

<세번째 시도 : 틀렸습니다.>

와... 될 줄 알았는데 안되네....

import sys

input = sys.stdin.readline

"""N개의 자연수의 합_N의 최댓값"""

S = int(input())

answer = 0

start = 0

cnt = []

while start < S:

    start += 1

    S -= start

    cnt.append(start)

   

if S not in cnt:

    print(len(cnt) + 1)

else:

    print(len(cnt))

 

<네번째 시도 : 맞았습니다.>

음... start가 증가하면서 while문의 거짓이 되는 조건이 start >= S인 조건인데 start가 +1씩 증가하는 상황에서

S가 cnt 리스트에 중복되는 수가 나올 리는 없다.

음... 결과적으로 어려운 문제는 아닌데 1부터 증가해서 모든 수를 더하거나 빼주는 생각을 빠르게 할 수 있는 방법이 있을까???

import sys

input = sys.stdin.readline

"""N개의 자연수의 합_N의 최댓값"""

S = int(input())

answer = 0

start = 0

cnt = []

while start < S:

    start += 1

    S -= start

    cnt.append(start)

   

print(len(cnt))

import sys

input = sys.stdin.readline

"""N개의 자연수의 합_N의 최댓값"""

S = int(input())

start = 0

cnt = 0

while start < S:

    start += 1

    S -= start

    cnt += 1

   

print(cnt)

 

 

<다른사람 코드 참고>

비슷한 방식으로 풀었다. 결국 1부터 시작해서 +1을 한다음에 누적되는 합계가 n보다 커질때를 활용해서 해결하는 방식이다.

즉, n = 200일 경우 더해지는 값들은 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19] 가 나올 것이고, 

sum을 하면 190이다. 200이 되기 위해서는 10이 모자란데 기존 리스트에 10이 있기 때문에 10 + 10 = 20이 될 것이고,

기존 리스트의 개수 19개에서 10을 빼고 20을 추가하면 개수는 19개로 동일하다.

 

다른 예시들도 동일하게 예상해본다.

n=int(input())

sum=0

cnt=0

for i in range(1, n+1):

  sum+=i

  cnt+=1

  if sum>n:

    cnt -= 1

    break

print(cnt)

 

일단 해당 문제가 그리디 알고리즘인지는 몰랐는데 설명을 보니 그리디 알고리즘이다.

 

[Chat GPT 도와줘]

그리디 알고리즘(Greedy Algorithm)은 매 선택에서 가장 좋은(최적의) 선택을 반복적으로 하는 방식으로 문제를 해결하는 알고리즘입니다. 그리디 알고리즘은 지역적으로 최적인 선택을 함으로써 전역적으로 최적의 해결책을 찾는 것이 목표입니다.

그리디 알고리즘의 특징

1. 현재 상황에서 최선의 선택을 함: 매 단계에서 가장 최적이라고 판단되는 선택을 합니다.
2. 미래에 대한 고려 없음: 이전 단계나 미래의 상황을 고려하지 않고, 현재 상태에서만 최적의 선택을 합니다.
3. 최적해 보장 조건: 모든 문제에서 그리디 알고리즘이 항상 최적해를 보장하는 것은 아닙니다. 문제에 따라 그리디 알고리즘으로 해결할 수 있기도 하고 없기도 합니다. 문제를 해결할 수 있는 경우는 그리디 선택 속성과 최적 부분 구조라는 조건을 만족해야 합니다.

그리디 알고리즘의 동작 과정

1. 문제를 작은 단위로 나눕니다.
2. 각 단계에서 최적의 선택을 반복하여 진행합니다.
3. 전체 문제 해결을 위한 해답을 구성합니다.

예시 1: 동전 거스름돈 문제

• 문제: 최소한의 동전 수로 거스름돈을 주기 위해 어떤 동전을 선택해야 하는가? 예를 들어, 500원, 100원, 50원, 10원짜리 동전이 있다고 할 때, 760원을 거슬러줘야 한다면 최소 동전의 개수는?

그리디 알고리즘 적용:

1. 가장 큰 동전부터 선택합니다.
2. 남은 금액에 대해 다시 가장 큰 동전을 선택합니다.

def min_coin_count(total, coins):

    count = 0

    for coin in coins:

        count += total // coin  # 해당 동전으로 거슬러 줄 수 있는 최대 개수

        total %= coin           # 남은 금액을 업데이트

    return count

coins = [500, 100, 50, 10]  # 동전 종류

total = 760                 # 거슬러줘야 할 금액

print(min_coin_count(total, coins))  # 출력: 4 (500원 1개, 100원 2개, 50원 1개, 10원 1개)

위 코드는 그리디 알고리즘을 사용하여, 가장 큰 동전부터 선택해 최소한의 동전 개수로 거스름돈을 줄 수 있는 방법을 찾아냅니다. 이 문제는 그리디 알고리즘으로 해결 가능한 전형적인 예입니다.

예시 2: 활동 선택 문제 (Activity Selection Problem)

• 문제: 일정 시간 동안 최대한 많은 활동을 하려면 어떤 활동을 선택해야 하는가? 각 활동은 시작 시간과 끝나는 시간이 주어져 있으며, 두 활동은 겹칠 수 없습니다.

그리디 알고리즘 적용:

1. 가장 빨리 끝나는 활동을 먼저 선택합니다.
2. 겹치지 않는 나머지 활동 중에서 다시 가장 빨리 끝나는 활동을 선택하는 과정을 반복합니다.

def max_activities(activities):

    # 끝나는 시간이 빠른 순서로 정렬

    activities.sort(key=lambda x: x[1])

   

    last_end_time = 0

    selected_activities = []

   

    for activity in activities:

        if activity[0] >= last_end_time:  # 현재 활동이 이전 활동과 겹치지 않으면 선택

            selected_activities.append(activity)

            last_end_time = activity[1]

   

    return selected_activities

activities = [(1, 3), (2, 5), (4, 6), (6, 8), (5, 7)]

print(max_activities(activities))  # 출력: [(1, 3), (4, 6), (6, 8)]

이 문제는 그리디 알고리즘이 최적의 해를 보장하는 대표적인 문제 중 하나입니다.

그리디 알고리즘의 장점과 단점

장점:

• 단순하고 직관적입니다.
• 빠른 실행 속도를 가집니다. 보통 그리디 알고리즘의 시간 복잡도는 O(N log N) 정도입니다.

단점:

• 항상 최적의 해를 보장하지는 않습니다. 그리디 알고리즘이 최적의 해를 구하려면, 문제 자체가 그리디 선택 속성과 최적 부분 구조를 가져야 합니다.
• 잘못된 선택을 할 수 있습니다. 현재는 최적의 선택처럼 보이지만, 이후의 선택에서 전체 최적해를 구하지 못할 수 있습니다.

그리디 알고리즘이 적합한 문제

• 동전 거스름돈 문제 (거스름돈 종류가 일정할 때)
• 활동 선택 문제
• 최소 신장 트리 문제 (Kruskal, Prim 알고리즘)
• 허프만 코딩 문제

요약

그리디 알고리즘은 매 단계에서 최적의 선택을 함으로써 전체 문제를 해결하는 알고리즘입니다. 하지만 모든 문제에서 그리디 알고리즘이 최적해를 보장하는 것은 아니기 때문에, 문제의 특성을 잘 파악하고 그리디 알고리즘이 적용 가능한지를 판단하는 것이 중요합니다.